GRAPHS IN DATA STRUCTURE
- Get link
- X
- Other Apps
GRAPHS
Graphs in data structures are non-linear data structures made up of a finite number of nodes or vertices and the edges that connect them. Graphs in data structures are used to address real-world problems in which it represents the problem area as a network like telephone networks, circuit networks, and social networks. For example, it can represent a single user as nodes or vertices in a telephone network, while the link between them via telephone represents edges.
What Are Graphs in Data Structure?
A graph is a non-linear kind of data structure made up of nodes or vertices and edges. The edges connect any two nodes in the graph, and the nodes are also known as vertices.
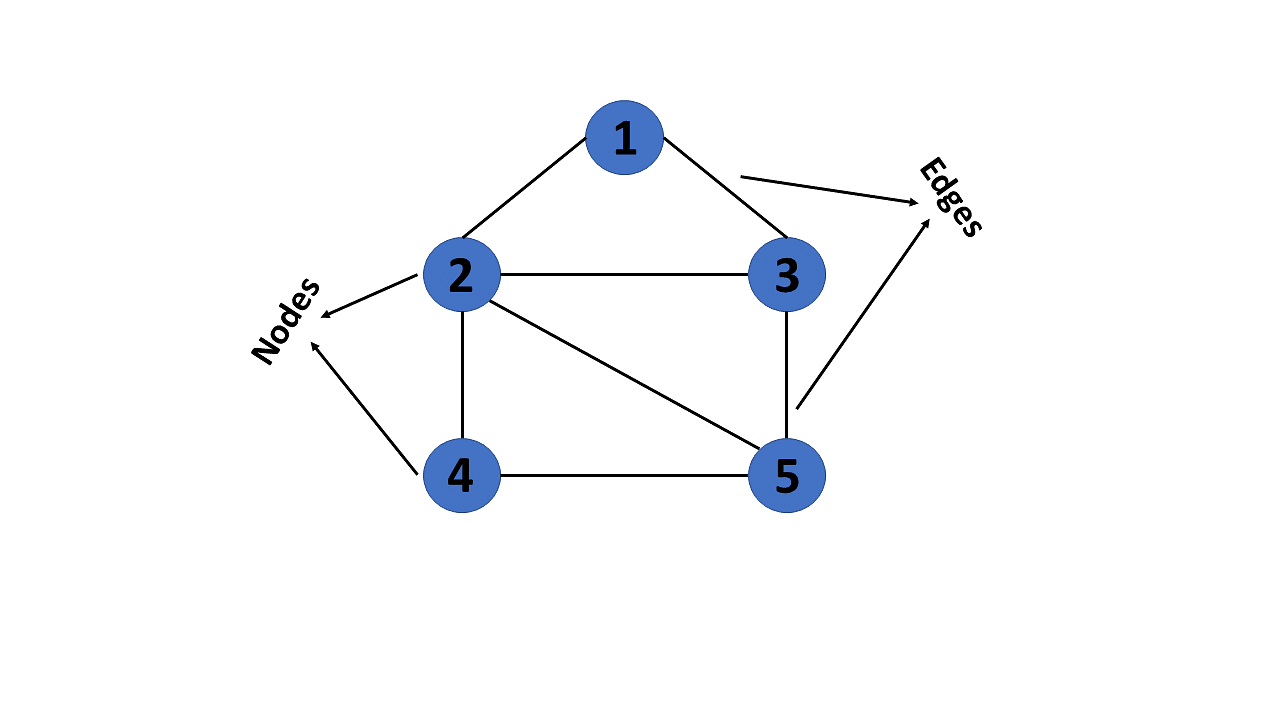
This graph has a set of vertices V= { 1,2,3,4,5} and a set of edges E= { (1,2),(1,3),(2,3),(2,4),(2,5),(3,5),(4,50 }.
Now that you’ve learned about the definition of graphs in data structures, you will learn about their various types.
Types of Graphs in Data Structures
There are different types of graphs in data structures, each of which is detailed below.
1. Finite Graph
The graph G=(V, E) is called a finite graph if the number of vertices and edges in the graph is limited in number
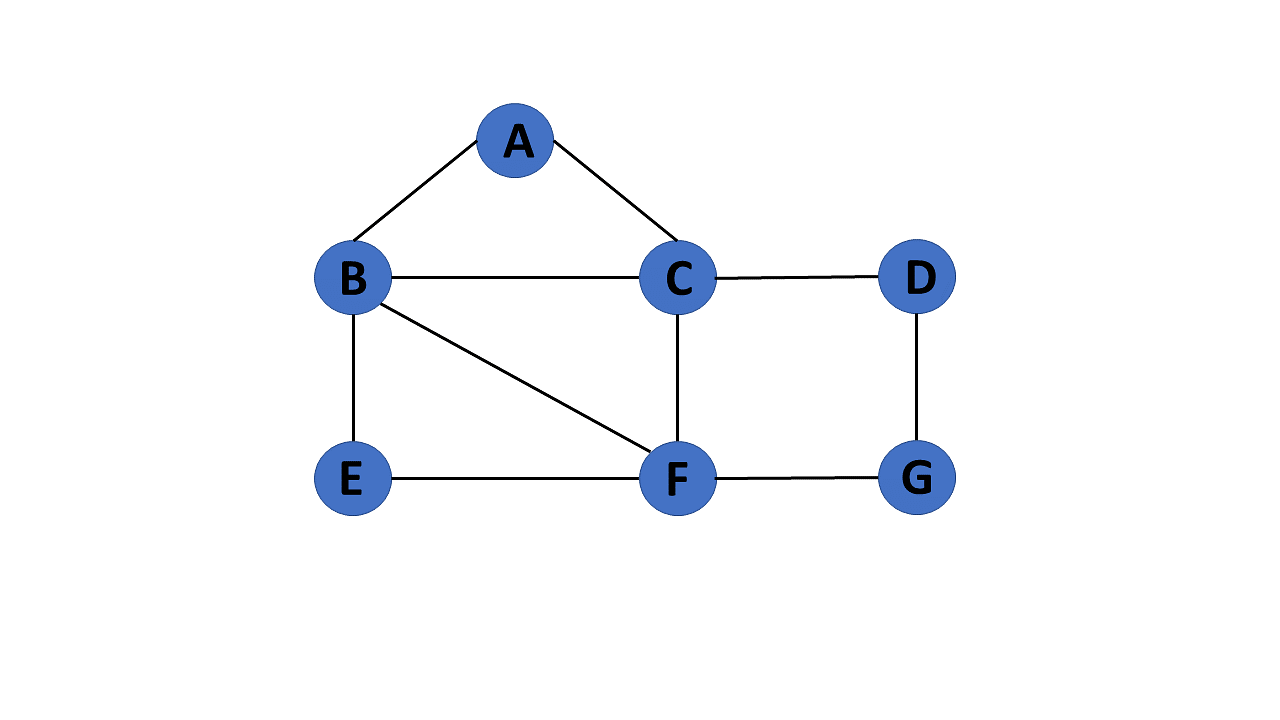
2. Infinite Graph
The graph G=(V, E) is called a finite graph if the number of vertices and edges in the graph is interminable.
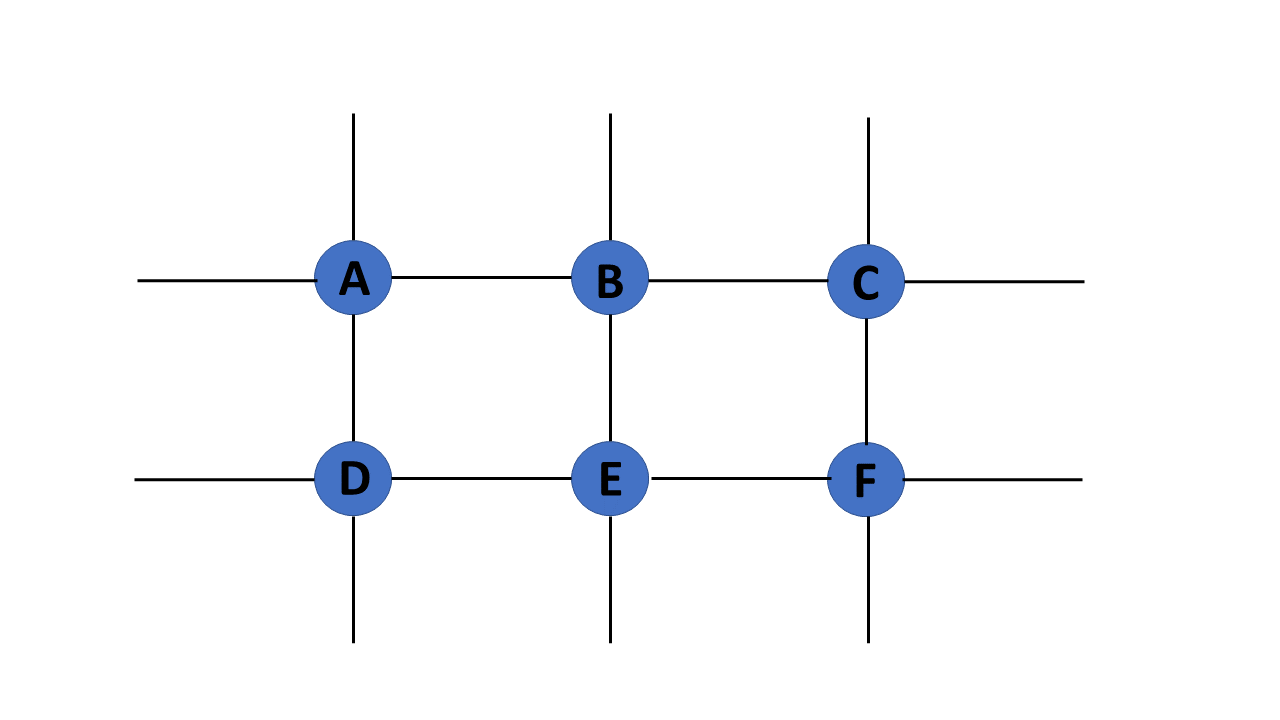
3. Trivial Graph
A graph G= (V, E) is trivial if it contains only a single vertex and no edges.

4. Simple Graph
If each pair of nodes or vertices in a graph G=(V, E) has only one edge, it is a simple graph. As a result, there is just one edge linking two vertices, depicting one-to-one interactions between two elements.
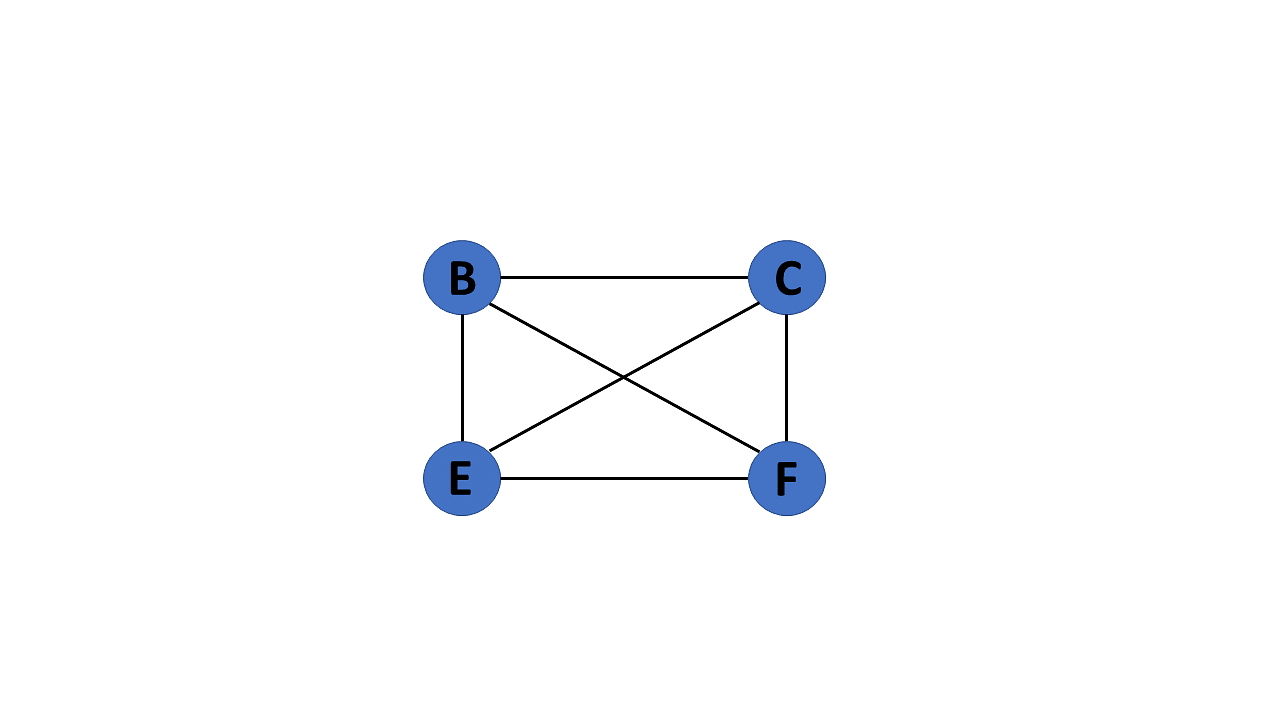
5. Multi Graph
If there are numerous edges between a pair of vertices in a graph G= (V, E), the graph is referred to as a multigraph. There are no self-loops in a Multigraph.
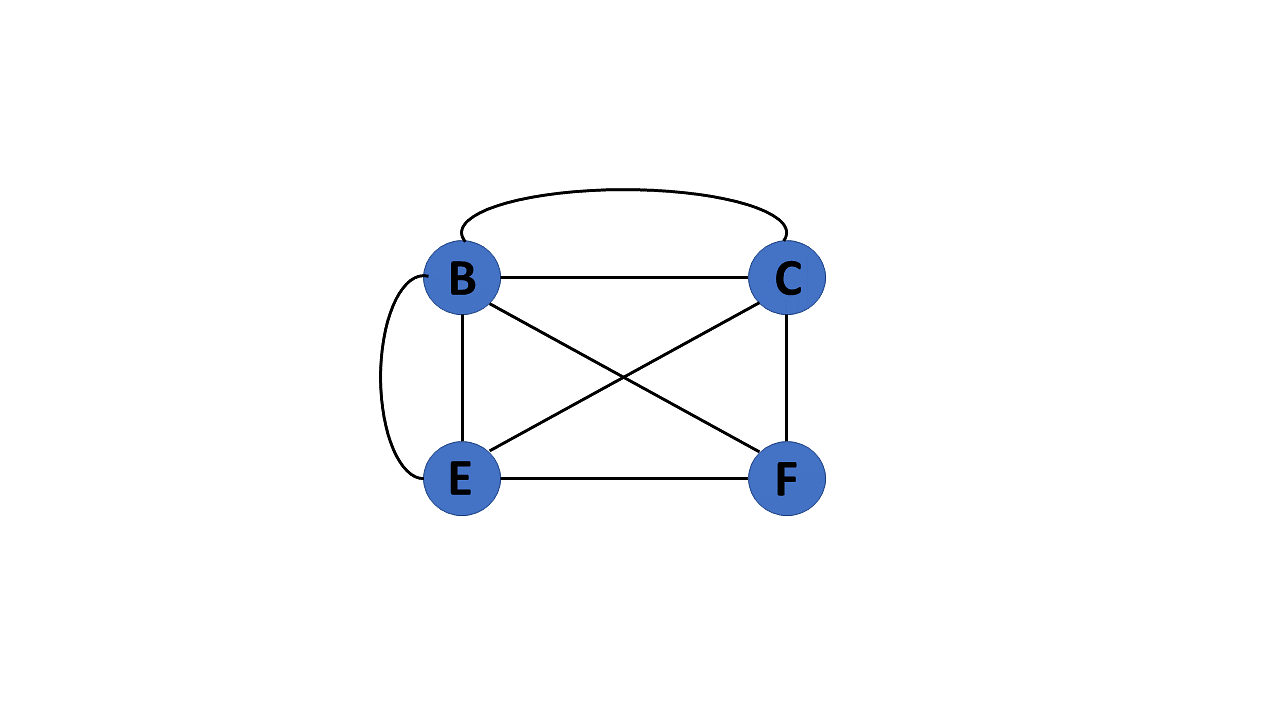
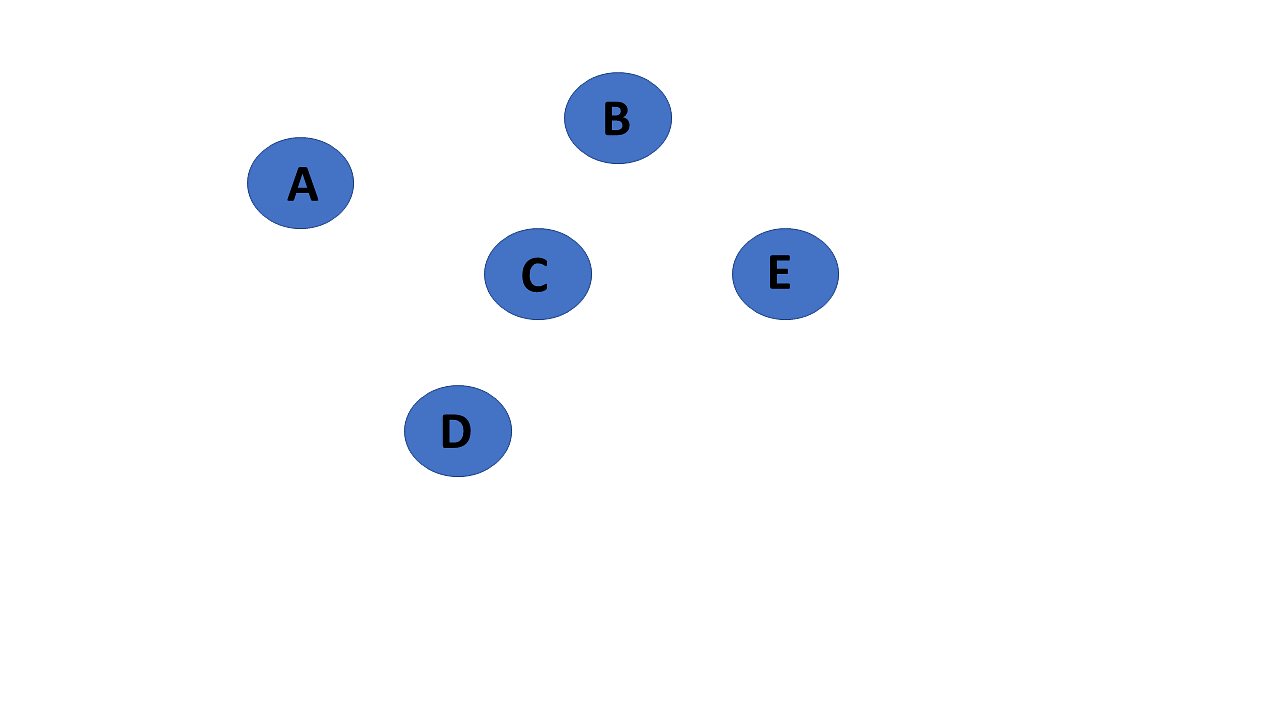
6. Null Graph
It's a reworked version of a trivial graph. If several vertices but no edges connect them, a graph G= (V, E) is a null graph.
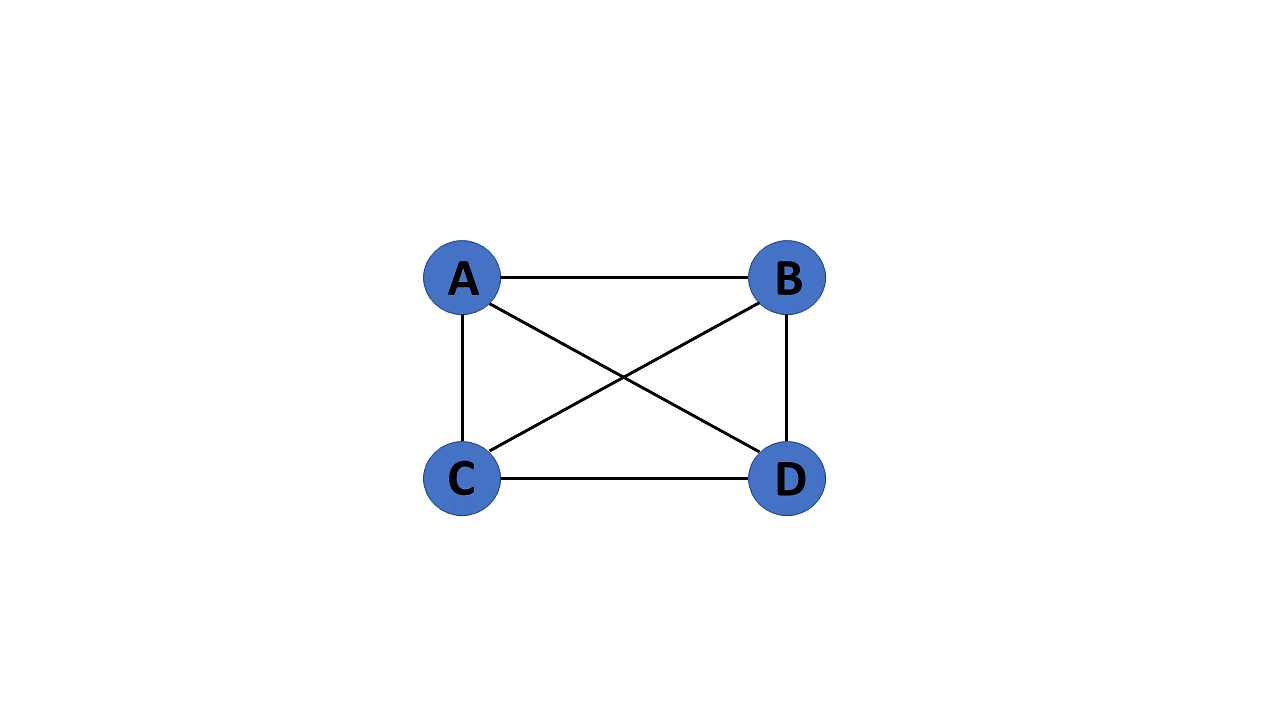
7. Complete Graph
If a graph G= (V, E) is also a simple graph, it is complete. Using the edges, with n number of vertices must be connected. It's also known as a full graph because each vertex's degree must be n-1.
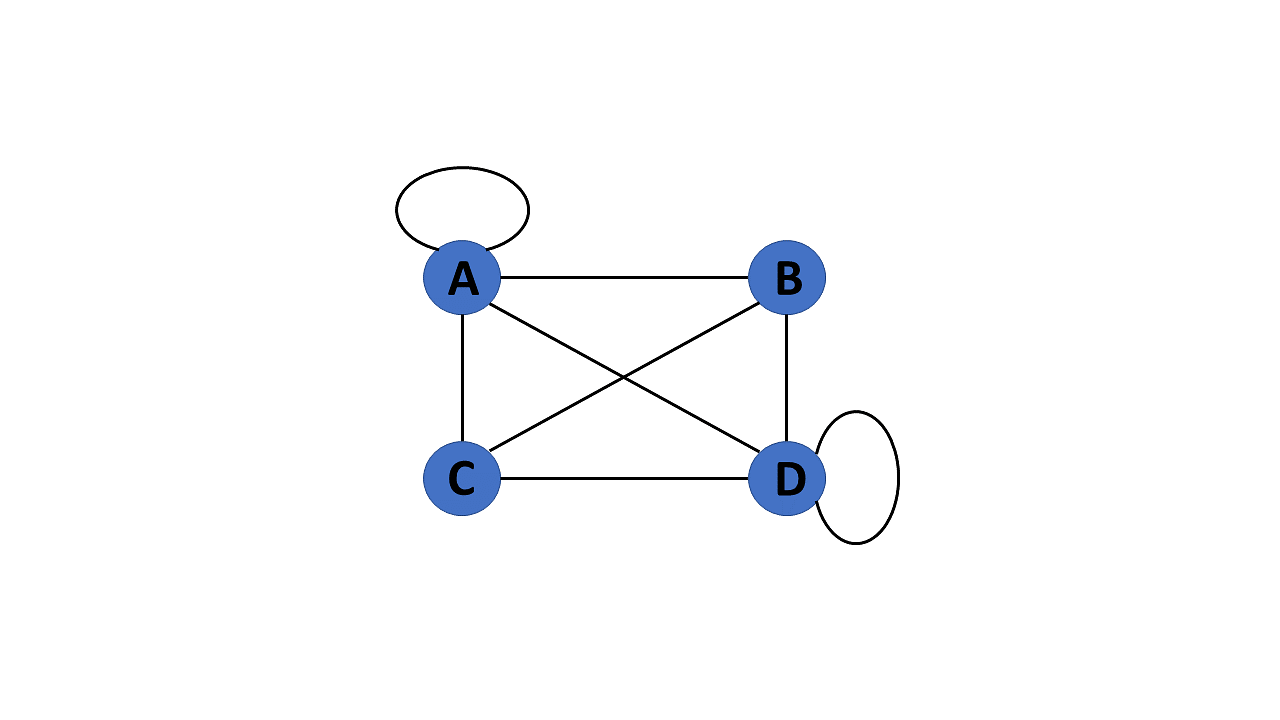
8. Pseudo Graph
If a graph G= (V, E) contains a self-loop besides other edges, it is a pseudograph.
9. Regular Graph
If a graph G= (V, E) is a simple graph with the same degree at each vertex, it is a regular graph. As a result, every whole graph is a regular graph.
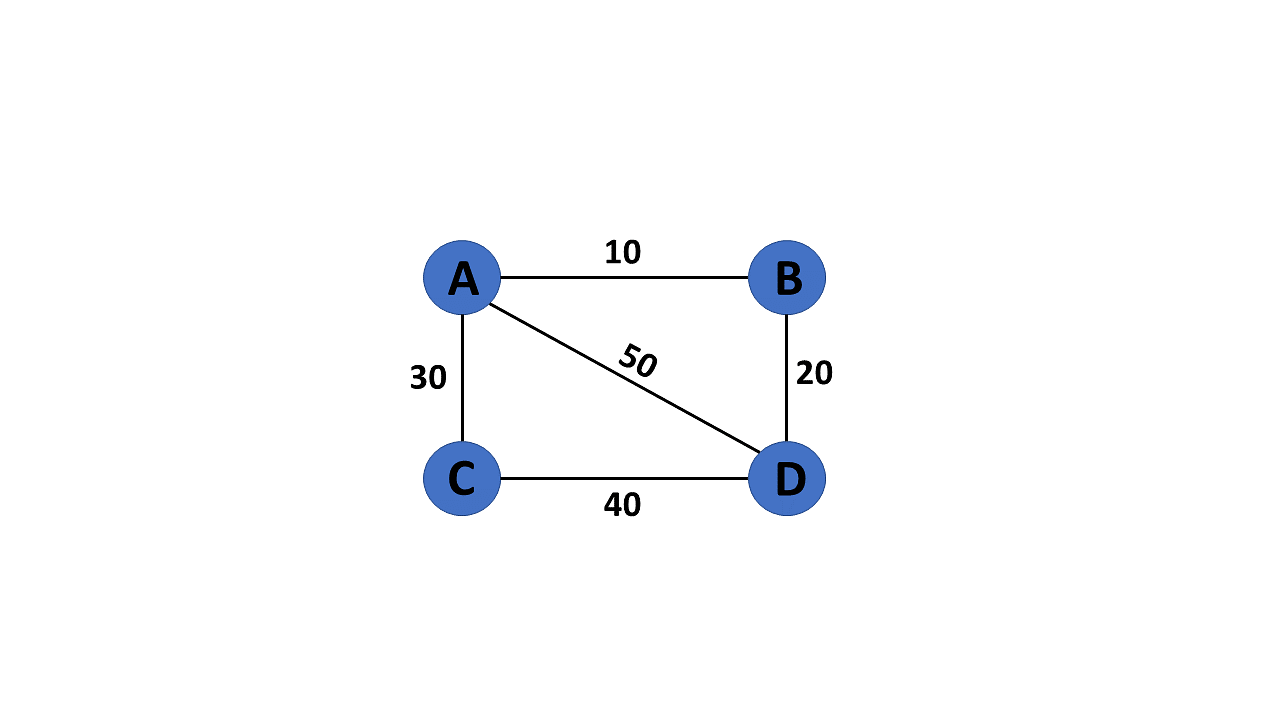
10. Weighted Graph
A graph G= (V, E) is called a labeled or weighted graph because each edge has a value or weight representing the cost of traversing that edge.
11. Directed Graph
A directed graph also referred to as a digraph, is a set of nodes connected by edges, each with a direction.
12. Undirected Graph
An undirected graph comprises a set of nodes and links connecting them. The order of the two connected vertices is irrelevant and has no direction. You can form an undirected graph with a finite number of vertices and edges.
13. Connected Graph
If there is a path between one vertex of a graph data structure and any other vertex, the graph is connected.
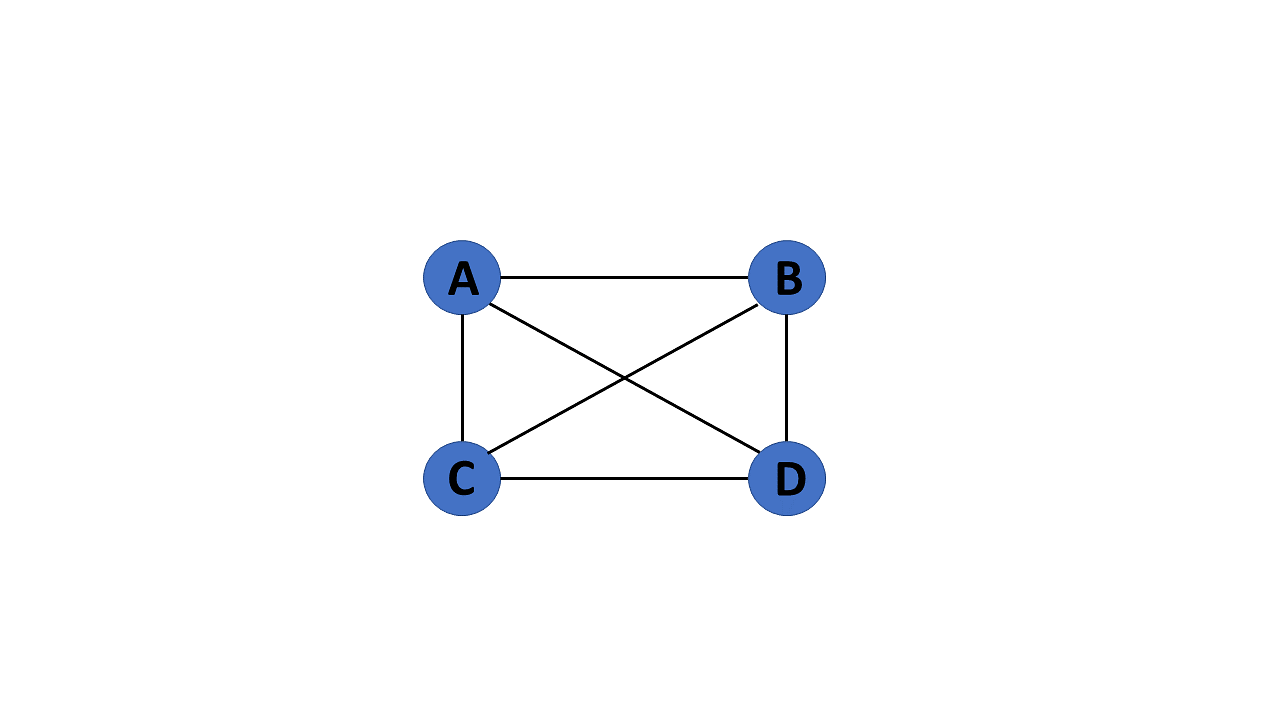
14. Disconnected Graph
When there is no edge linking the vertices, you refer to the null graph as a disconnected graph.
![]()
15. Cyclic Graph
If a graph contains at least one graph cycle, it is considered to be cyclic.
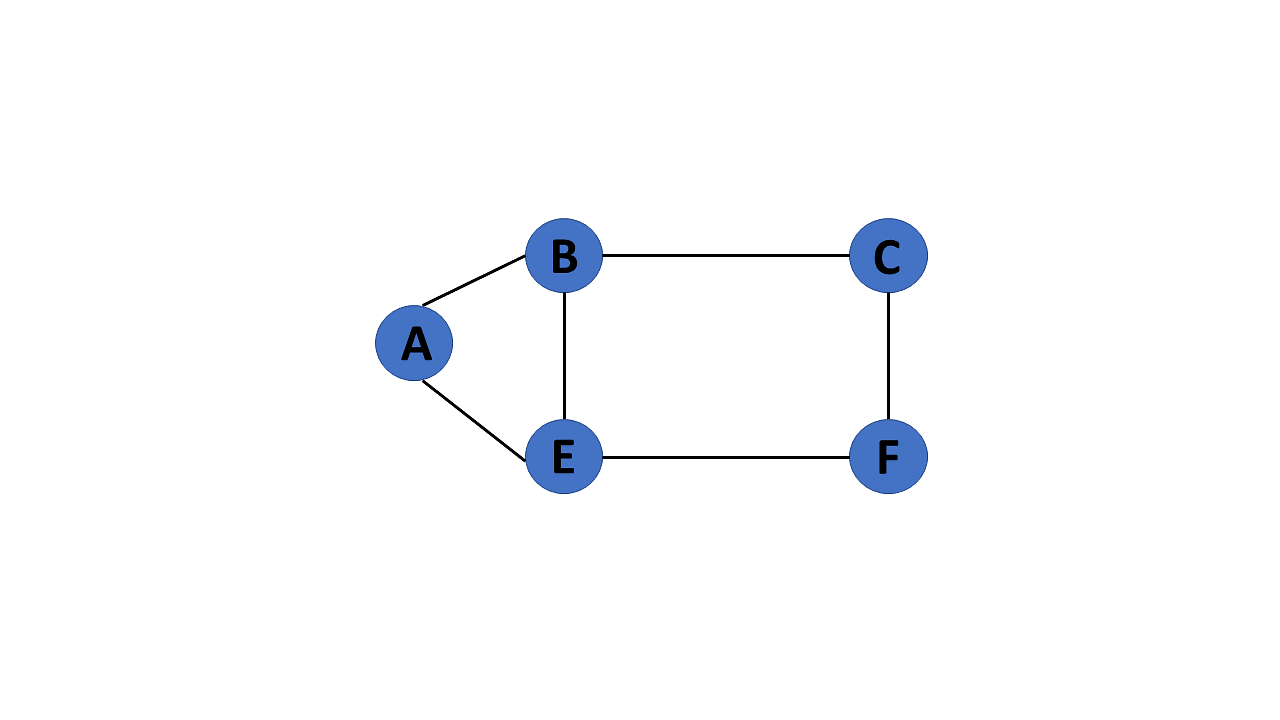
16. Acyclic Graph
When there are no cycles in a graph, it is called an acyclic graph.
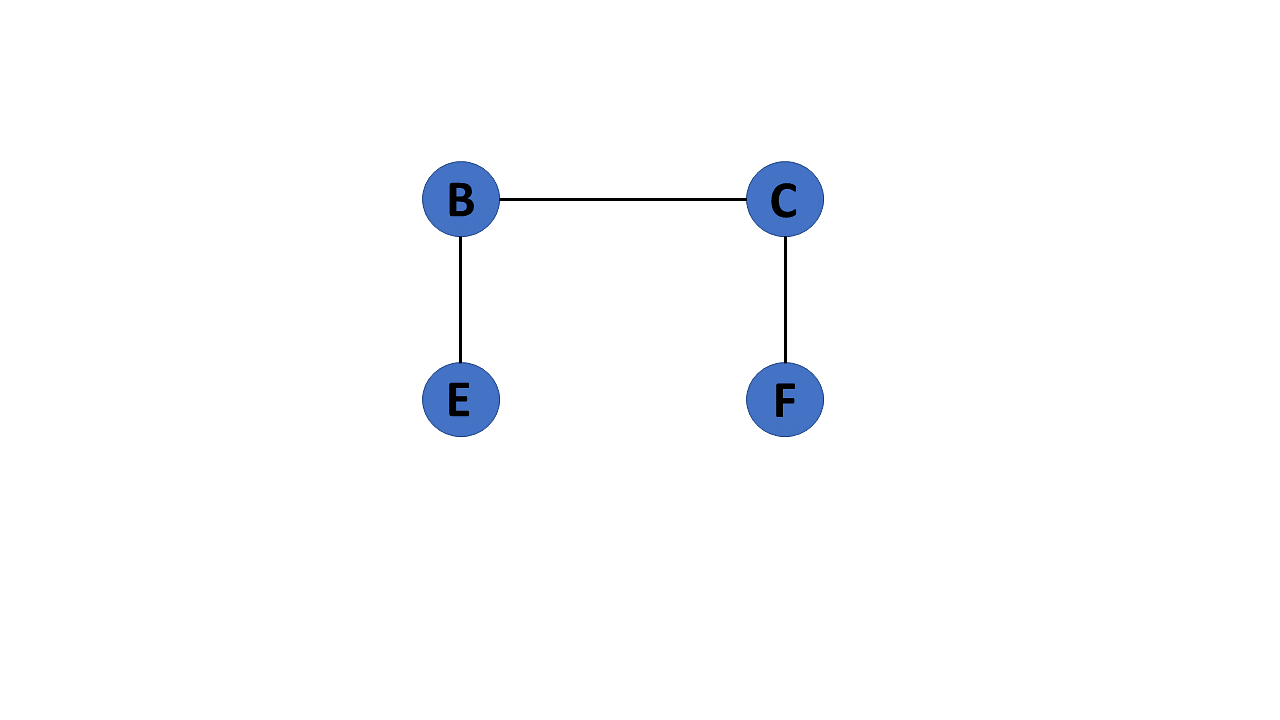
17. Directed Acyclic Graph
It's also known as a directed acyclic graph (DAG), and it's a graph with directed edges but no cycle. It represents the edges using an ordered pair of vertices since it directs the vertices and stores some data.
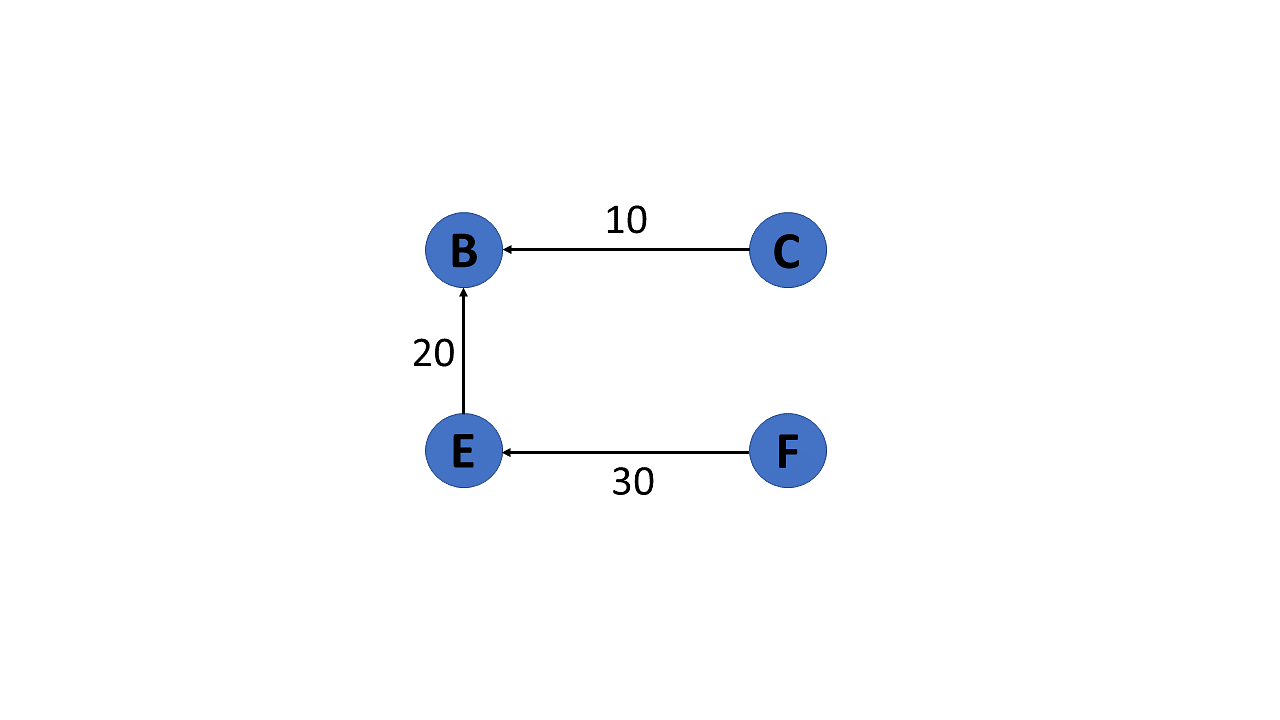
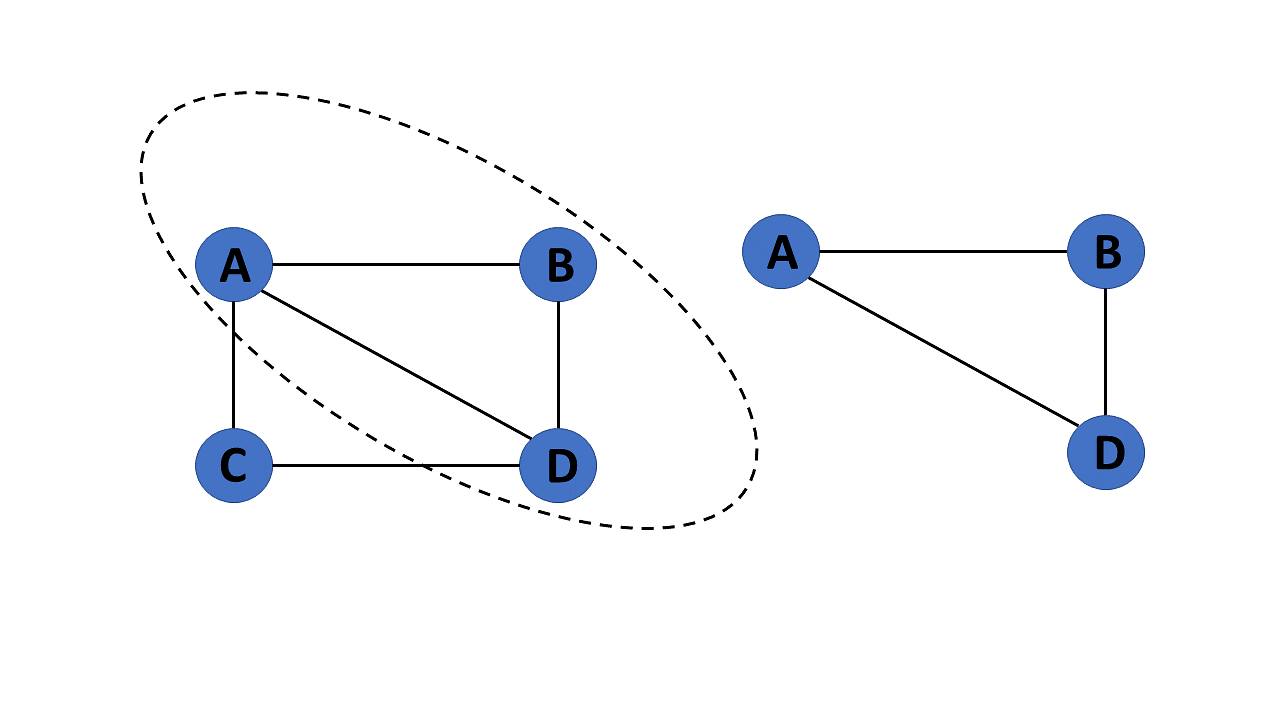
18. Subgraph
The vertices and edges of a graph that are subsets of another graph are known as a subgraph.
B.BHASKI
23BK1A05K8
- Get link
- X
- Other Apps
Comments